Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
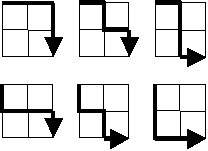
How many such routes are there through a 20×20 grid?
网格路径
从一个 2*2 网格的左上角出发,若只允许向右或向下移动,则恰好有 6 条抵达右下角的路径。
对于 20*20 网格,这样的路径有多少条?
对于边长为 n 的网格,从左上角到右下角共有 2*n 条边需要走。如果我们确定了每一步向右所在的位置,那么我们就完全确定了整个路线。我们可以写出这样的代码:
(defun eu15-f (n st)
(if (= n 0) 1
(cl-loop for i from 0 to st
sum (eu15-f (- n 1) i))))
(eu15-f 20 20)
;; another representation
(defun eu15-f1 (m n)
(if (or (= m 0) (= n 0)) 1
(+ (eu15-f1 m (1- n))
(eu15-f1 (1- m) n))))
这段代码的意思是从左上向右下一个一个选择向右移动的线段位置在整个网格的位置。由于复杂度太高而无法计算,我们需要采用类似动态规划的方法,对于给定点 (i,j) 从左上角到达该点的方式为从左上到达 (i,j-1) 和 (i-1,j) 的方式之和。由此我们可以这样做:
(defun eu15-f2 (n)
(let ((vec (make-vector (1+ n) -1)))
(cl-loop for i from 0 to n
do (aset vec i (make-vector (1+ n) -1)))
(cl-loop for i from 0 to n
do (aset (aref vec 0) i 1)
do (aset (aref vec i) 0 1))
(cl-loop for i from 1 to n
do (cl-loop for j from 1 to n
do (aset (aref vec i) j
(+ (aref (aref vec (1- i)) j)
(aref (aref vec i) (1- j))))))
(aref (aref vec n) n)))
(eu15-f2 20)
;; 137846528820最后奉上一种组合数学的解决方式。如上所述,我们只要完全确定了向右走的线段,我们就可以完全确定向下走的线段。这个问题就等价于使用各 N 个字母 D 和 R 来填充长度为 2N 的字符串,或者说是把 N 个球放到 2*N 个洞中。这就等价于从 2*N 个洞中选出 10 个洞,即 C(2N, N)。
(defun eu15-C (n m)
(cl-labels ((fac (n)
(cl-reduce '* (number-sequence 1 n))))
(/ (fac n) (fac m) (fac (- n m)))))
(eu15-C 40 20)
;; 137846528820