CPS and Cont Monad — The Mother of all Monads

在数学中，将两个或多个函数嵌套起来可以得到一个新的函数，这也叫函数复合 (function composition)，比如 \(f(x) = sin(cos(x))\)。在计算这个函数时，参数 \(x\) 首先会作为 \(cos\) 函数的输入，随后 \(cos(x)\) 的值会作为 \(sin\) 的输入，完成整个计算过程。我们通过函数的数学表达式直观地定义并执行了复合函数的求值步骤。

在编程语言中，我们要怎样实现将函数的返回值传递给「之后」的函数呢？为了回答这个问题，不妨先看看那些不支持函数嵌套的语言是怎么解决的（虽然 CMake 提供了 math ，但这里我们关注的是函数嵌套的实现方式）：

cmake_minimum_required(VERSION 3.30)

project(math)

function (Add a b result)
  math(EXPR value "${a} + ${b}")
  set(${result} ${value} PARENT_SCOPE)
endfunction()

set(res 0)

# (+ (+ 1 2) 3)
Add(1 2 res)
Add(${res} 3 res)

message("The result is : ${res}")

# The result is : 6
# -- Configuring done (4.7s)
# -- Generating done (0.0s)
# -- Build files have been written to: ...

由于 CMake 中的函数不支持直接返回值，我们只能先将计算结果存储在变量中，再通过变量参后续的调用。基于这一限制，在实现简单计算器时，我们可以按照「由内到外」的顺序，先对内层表达式求值，将结果绑定到一个变量，然后利用这个变量完成后续的计算过程：

#lang racket

(define (inter S)
  (match S
    [(? number?) S]
    [(list '+ s1 s2)
     (let ([a (inter s1)] [b (inter s2)])
       (+ a b))]
    [(list '- s1 s2)
     (let ([a (inter s1)] [b (inter s2)])
       (- a b))]
    [_ (error "error")]))

除了显式使用变量传递参数外，我们还可以利用栈来完成参数传递。在 WebAssembly (WASM) 中，调用约定非常简单： call 指令会从栈中消耗参数并将其传递给被调用函数，被调者的返回值会被压入栈中。在这种调用约定下，WASM 运行时负责清理栈，栈主要用于参数的传递和返回值的管理。

The call instruction invokes another function, consuming the necessary arguments from the stack and returning the result values of the call.

Instructions — WebAssembly 2.0 (Draft 2024-12-18)

以下是一个在 WASM 中实现简单数学表达式计算的示例（如你所见，在 WAT 格式中指令甚至可以嵌套）：

(module
  (func $add (param i32 i32) (result i32)
    local.get 0 local.get 1 i32.add)
  (func $sub (param i32 i32) (result i32)
    (i32.sub (local.get 0) (local.get 1)))
  (func (export "calc") (result i32)
    i32.const 1 i32.const 2 call $add
    i32.const 3 call $sub)
  (func (export "calc2") (result i32)
    (call $sub (call $add (i32.const 1) (i32.const 2)) (i32.const 3))))

// also check https://webassembly.github.io/wabt/demo/wat2wasm/

let wCode = 'AGFzbQEAAAABCwJgAn9/AX9gAAF/AwUEAAABAQcQAgRjYWxjAAIFY2FsYzIAAworBAcAIAAgAWoLBwAgACABawsMAEEBQQIQAEEDEAELDABBAUECEABBAxABCwAdBG5hbWUBCwIAA2FkZAEDc3ViAgkEAAABAAIAAwA='

function base64ToArrayBuffer(base64) {
    var binaryString = atob(base64);
    var bytes = new Uint8Array(binaryString.length);
    for (var i = 0; i < binaryString.length; i++) {
        bytes[i] = binaryString.charCodeAt(i);
    }
    return bytes.buffer;
}

const {instance} = await WebAssembly.instantiate(
    base64ToArrayBuffer(wCode), {})
const {calc, calc2} = instance.exports

console.log(calc())
console.log(calc2())

只要根据 S-exp 计算表达式编译到 WAT 格式，我们就算通过栈实现了嵌套表达式的求值。

(A '(+ 1 (+ 2 3)))
;; => (let* ((t0 (+ 2 3)) (t1 (+ 1 t0))) t1)
;; or (let ((t0 (+ 2 3))) (let ((t1 (+ 1 t0))) t1))

(define (A S)
  (if (atom? S)
      `((,S))
      ...))

#lang racket

(define (atom? s)
  (not (or (cons? s) (null? s))))
(define (A0 S)
  (if (atom? S)
      `((,S))
      (g S '() '())))

(define (g ls elements result)
  (cond
    ((null? ls)
     (let* ((cl (reverse elements))
            (op (gensym)))
       (cons (list op cl) result)))
    (else
     (let* ((ele (car ls))
            (res0 (A0 ele))
            (res1 ; an atom value
             (if (= (length (car res0)) 1)
                 (cdr res0) res0)))
       (g (cdr ls) (cons (caar res0) elements)
          (append res1 result))))))

(define (A S)
  (let ((res (A0 S)))
    (if (and (= (length res) 1)
             (= (length (car res)) 1))
        (caar res)
        `(let* ,(reverse res) ,(caar res)))))

(A '(+ 1 (+ 2 (* 2 3)) (/ 3 3))) ;;=>
#|
'(let* ((g301307 (* 2 3))
        (g301308 (+ 2 g301307))
        (g301309 (/ 3 3))
        (g301310 (+ 1 g301308 g301309)))
   g301310)
|#

#lang racket

(define (A S)
  (define gs
    (let ((cnt 0))
      (λ ()
        (let* ((num (number->string cnt))
               (str (string-append "t" num))
               (sym (string->symbol str)))
          (set! cnt (+ cnt 1))
          sym))))
  (define res
    (let F ([s S])
      (if (or (not (cons? s)) (eq? (car s) 'quote))
          `((,s))
          (let g ([ls s] [slist '()] [res '()])
            (cond
              ((null? ls)
               (let ((rls (reverse slist))
                     (smb (gs)))
                 (cons (list smb rls) res)))
              (else
               (let* ((item (car ls))
                      (fr (F item))
                      (fr* (if (= (length (car fr)) 1) (cdr fr) fr)))
                 (g (cdr ls) (cons (caar fr) slist) (append fr* res)))))))))
  (if (and (= 1 (length res))
           (= 1 (length (car res))))
      (caar res)
      (list 'let* (reverse res) (caar res))))

(A '(+ 1 (+ 2 (* 2 3)) (/ 3 3))) ;;=>
;; '(let* ((t0 (* 2 3)) (t1 (+ 2 t0)) (t2 (/ 3 3)) (t3 (+ 1 t1 t2))) t3)

(let* ((t0 (* 2 3)) (t1 (+ 2 t0)) (t2 (/ 3 3)) (t3 (+ 1 t1 t2))) t3)
;; => 10

#lang racket
(require racket/control)

(define (A* term)
  (define gs
    (let ((cnt 0))
      (λ ()
        (let* ((num (number->string cnt))
               (str (string-append "t" num))
               (sym (string->symbol str)))
          (set! cnt (+ cnt 1))
          sym))))
  (reset
   (let F ([s term])
     (match s
       ((list 'quote v) v)
       ((cons t1 tN)
        (shift k (let ((t (gs)))
                   (list 'let
                         `((,t
                            ,(map F (cons t1 tN))))
                         (k t)))))
       ((var v) v)))))

(A* '(+ 1 (+ 2 (* 2 3)) (/ 3 3))) ;;=>
;'(let ((t2 (* 2 3))) (let ((t1 (+ 2 t2))) (let ((t3 (/ 3 3))) (let ((t0 (+ 1 t1 t3))) t0))))

(let ((t2 (* 2 3))) (let ((t1 (+ 2 t2))) (let ((t3 (/ 3 3))) (let ((t0 (+ 1 t1 t3))) t0))))
;; => 10

无论是通过变量保存表达式的值，还是使用栈存储表达式的值，我们都能实现「对嵌套表达式的求值」。从另一个角度来看，计算过程的组合不仅依赖计算本身，还需要一个额外的机制，我们叫它计算的续体 (continuation)。续体的作用在于告诉程序“计算的结果应该传递到哪里去”，从而在控制流中扮演关键角色。

在函数式语言中，程序本质上是由一系列嵌套表达式构成的，通过逐层求值最终生成结果。从这个意义上说，续体是将这些表达式有序连接在一起的核心工具，它定义了每一步计算的执行顺序和结果传递方式。

在编程语言层面，程序的续体是一种抽象，表示程序执行到某个点剩余的计算。大多数编程语言的运行时通过调用堆栈来管理续体，函数的调用和返回被视为栈上的进出操作。而某些语言（如 Scheme）直接支持续体，允许程序员捕获当前计算状态并以对象的形式存储起来，稍后再恢复。

The Scheme Programming Language 第三章第三小节是这样介绍续体的：

在对 Scheme 表达式求值时，Scheme 实现必须搞清楚两件事：

1. 对什么进行求值（what to evaluate）
2. 如何处理这个值（what to do with the value）

我们将 如何处理这个值 称为某个 表达式求值 的 continuation。

理解了这两句话就明白什么是续体了。

在上面的 inter 函数中，被解释的代码并不清楚自身的求值过程。续体的概念在代码层面是隐式的，常见的编程语言倾向于使用「控制流」而非「续体」的概念，并通过诸如 while, for, continue 和 break 等控制关键字来有限地操控程序流程。那么，有没有什么方法能够在语言层面显式地使用续体呢？答案是肯定的，这就是 CPS (Continuation-passing style) 。在支持一等函数的语言中，可以将续体传递为函数参数，从而使用 CPS 风格的代码来捕获并操作程序的控制流。

续体的本质是「后续计算」，我们可以使用函数来表示它。对于表达式 (+ 1 (+ 2 3)) ，子表达式 (+ 2 3) 的续体可以表示为 (λ (x) (+ 1 x)) 。原表达式可以转换为 ((λ (x) (+ x 1)) (+ 2 3)) 。我们初步实现了显式暴露续体的目的，但这还不够通用。如果 (+ 2 3) 的后续计算是“加二”，“加三”或其他操作呢？为了更抽象地表达这种变化，可以将 (λ (x) (+ x 1)) 抽象为一个变量 k ，得到 (k (+ 2 3)) 。现在，在外层添加 λ (k) 并调整调用顺序，我们就得到了 ((λ (k) (k (+ 2 3))) (λ (x) (+ x 1))) 。

在 Racket 中，上述表达式的值为 6。这种将表达式转换为接受并调用续体参数形式的代码叫做 CPS 风格代码，是一种利用续体思想的编程风格。CPS 代码的一个显著特性是：在「严格」CPS 转换中，除语言本身提供的内置函数外， 所有的函数调用都必须是尾调用 。尾调用指的是函数在执行的最后一步调用另一个函数，并 直接 返回该函数的返回值，而无需保留当前函数的调用栈。尾调用的这一特性使得编译器或解释器可以进行尾调用优化，从而避免栈溢出。尾调用优化 (Tail Call Optimisation, TCO) 几乎是所有函数式语言的标配。

在以下代码示例中， f 是尾调用而 g 不是，因为它在结尾处调用的 * 要等待子表达式 (g (- n 1)) 的返回：

#lang racket

(define (f n res)
  (if (= n 0) res (f (- n 1) (* res n))))
(define (g n)
  (if (= n 0) 1 (* n (g (- n 1)))))

我们可以通过让函数接受一个额外的续体参数，使其能够在函数内部直接将计算结果传递给续体。例如， CPS 化的 car 函数可以表示为 (λ (x k) (k (car x)) 。通过使用 CPS 化的 + ， (+ 1 (+ 2 3)) 可以变换为 (+* 2 3 (λ (v) (+ v 1)))) 。这种转换要求我们手动将嵌套表达式分解为一系列显式的函数调用。这不仅实现了嵌套表达式的求值，也使程序的控制流完全显式化。

(((λ (k) (k '((1 2))))
  (λ (x) (λ (k) (k (car x)))))
 car)

((λ (k) (k '((1 2)) car))
 (λ (x k) (k (car x))))

(define (+* a b k) (k (+ a b)))
(define (-* a b k) (k (- a b)))
(define (** a b k) (k (* a b)))
(define (/* a b k) (k (/ a b)))

(** 2 3
    (λ (v1)
      (+* v1 3
          (λ (v2)
            (/* 3 3
                (λ (v3)
                  (-* v3 1
                      (λ (v4)
                        (+ v2 v4)))))))))

利用续体参数，我们可以实现一些有趣的功能，例如函数式的 break 。（如果编程语言不支持尾递归优化，不建议使用这种方法来表示循环。）

((λ (break)
  (let loop ([i 1] [sum 0])
    (cond
      ((= i 100) sum)
      (else
       (if (= i 50) (break sum)
           (loop (+ i 1) (+ sum i)))))))
 identity) ;;=>
;; 1225 (0 + 49) * 50 / 2

#lang racket

(define (product ls k)
  (let f ([ls ls] [k0 k])
    (match ls
      ['() (k0 1)]
      [(cons 0 b) (k 0)]
      [(cons a b) (begin (display a) (f b (λ (v) (k0 (* a v)))))])))
(product '(1 2 0 3) list)
;; => 12'(0)

#lang racket

(define (product ls)
  (call/cc (lambda (k)
             (let f ([ls ls])
               (match ls
                 ['() 1]
                 [(cons 0 b) (k 0)]
                 [(cons a b) (* a (f b))])))))
(product '(1 0 2))
;; => 0
(product '(1 2 3))
;; => 6

#lang racket

(define CPS (λ (f) (λ args (λ (k) (k (apply f args))))))
;; functions
(define *C (CPS *))
(define null?C (CPS null?))
(define carC (CPS car))
(define cdrC (CPS cdr))
(define zero?C (CPS zero?))

(define (product ls)
  (λ (ka)
    (define (fC ls)
      (λ (k0)
        ((null?C ls)
         (λ (v1)
           (if v1 (k0 1)
               ((carC ls)
                (λ (v2)
                  (display v2)
                  ((zero?C v2)
                   (λ (v3)
                     (if v3 (ka 0)
                         ((carC ls)
                          (λ (v4)
                            ((cdrC ls)
                             (λ (v5)
                               ((fC v5)
                                (λ (v6)
                                  ((*C v4 v6) k0)))))))))))))))))
    ((fC ls) ka)))
((product '(1 2 3)) list)
;; => 123'(6)
((product '(1 0 2)) list)
;; => 10'(0)

由于 CPS 风格的代码通过连续的续体调用来组织程序流程，代码的结构从传统的树状嵌套变为线性链式结构。在完全 CPS 化的代码中，函数调用不再依赖调用栈的嵌套，而是完全依赖于续体参数的传递。由于所有的控制流都显式地通过续体函数进行管理，CPS 代码通常比非 CPS 代码更难理解和维护。

本节从嵌套表达式入手，逐步阐释了嵌套表达式背后的原理，并将其推广到续体的概念。随后，我们介绍了如何使用 CPS 捕捉续体，以及如何利用 CPS 做一些简单的控制流操作。希望读者通过本节能回顾并熟悉续体和 CPS 的概念。我原本计划在本节介绍 call/cc 及其常见用法，比如用call/cc合成所有的控制流结构。但考虑到 Haskell 中也存在 Cont Monad 和 callCC ，下面我们迟早会接触到，此处暂不赘述。

虽然函数调用可以嵌套，但在实践中我们通常会避免深度嵌套，因为嵌套难以 debug。

在练习 3 最后的 product 实现中，我给出了函数 CPS 转换的如下定义：

(define CPS (λ (f) (λ args (λ (k) (k (apply f args))))))

然而，这是一个相当“浅”的变换，生成的函数在调用时其内部并不一定是 CPS 的。如果我们对代码本身而不是不透明的函数对象进行 CPS 变换，那么毫无疑问，这将是一个递归的过程：

由于本文的重点不在 CPS 变换和玩 Racket 上，这里给出一些讲解 CPS 变换的文章：

• emacs generator 使用及实现介绍 — 一个简单的 CPS 变换实现
• CPS 变换与 CPS 变换编译 by 梨梨喵
• How to compile with continuations by matt might
• Into CPS, never to return，使用 Python 实现，简单易懂

在静态类型的 Haskell 中，实现一个单子意味着创建一个 Monad 类型类的实例，比如 Maybe ：

-- https://learnyouahaskell.github.io/a-fistful-of-monads.html
instance Monad Maybe where
  return x = Just x
  Nothing >>= f = Nothing
  Just x >>= f  = f x
  fail _ = Nothing

在上面的 Maybe 例子中， Maybe 本身是一个类型构造器，我们为它实现了 return 和 >>= 运算符（由于本文讨论的论文未涉及 fail ，此处略过）。这两个运算符对应于上述定义中的 unitM 和 bindM 。在动态类型语言中，“类”的概念约等于类型构造器，而单子可以视为一种接口。我们只需创建支持对应接口的“类”，即可认为实现了一个单子。我们甚至不必局限于创建新的“类”，而是使用已有的数据结构（例如列表，数组或元组），并为其提供相应的接口函数。

在实现这些接口函数时，除了满足 unitM 和 bindM 的类型签名要求外，还需要满足单子定律，包括单位元律（Left Identity）、右单位元律（Right Identity）和结合律（Associativity）：

#lang racket

(define-values (returnID >>= ID)
  (values
   (λ (x) (new ID [value x]))
   (λ (obj f) (send obj bindM f))
   (class object%
     (super-new)
     (init value)
     (define v value)
     (define/public (get) v)
     (define/public (bindM f) (f v)))))

(define ID-eq?
  (λ (o1 o2)
    (equal? (send o1 get) (send o2 get))))

(ID-eq? (>>= (returnID 1) (λ (x) (returnID (add1 x))))
        ((λ (x) (returnID (add1 x))) 1))
(ID-eq? (>>= (returnID 1) returnID)
        (returnID 1))
(ID-eq? (>>= (returnID 1) (λ (x)
                            (>>= (returnID (add1 x))
                                 (λ (x) (returnID (* x 2))))))
        (>>= (>>= (returnID 1) (λ (x) (returnID (add1 x))))
             (λ (x) (returnID (* x 2)))))

除了 unitM 和 bindM 外，单子也可以使用 unitM, mapM 和 joinM 定义：

#lang racket

(define unitM (λ (x) (list x)))
(define mapM (λ (f) (λ (x) (map f x))))
(define joinM (λ (v) (apply append v)))
(define bindM (λ (obj k) (joinM ((mapM k) obj))))

(equal? ((mapM identity) '(1 2 3))
        (identity '(1 2 3)))
(define f (λ (x) (add1 x)))
(define g (λ (x) (* x 2)))
(equal? ((mapM (λ (x) (f (g x)))) '(1 2 3))
        ((mapM f) ((mapM g) '(1 2 3))))

(equal? ((mapM f) (unitM 1)) (unitM (f 1)))
(equal? ((mapM f) (joinM '((1) (2))))
        (joinM ((mapM (mapM f)) '((1) (2)))))

(equal? (joinM (unitM 1)) 1)
(equal? (joinM ((mapM unitM) '(1 2 3)))
        '(1 2 3))
(equal? (joinM ((mapM joinM) '(((1)) ((2)))))
        (joinM (joinM '(((1)) ((2))))))
(equal? (bindM '(1 2) (λ (x) (unitM f)))
        (joinM ((mapM (λ (x) (unitM f))) '(1 2))))

在上一节的练习 2 中，我们通过将续体参数置于函数的最后一个参数来编写 CPS 风格的代码。然而，这种风格的代码似乎缺乏组合型，我们无法轻易地将其从中间截断，因为这样做可能会导致无法访问某些闭包变量：

(** 2 3
    (λ (v1)
      (+* v1 3
          (λ (v2)
            (/* 3 3
                (λ (v3)
                  (-* v3 1
                      (λ (v4)
                        (+ v2 v4)))))))))

在上面的代码中， v2 和 v4 直到计算的最后阶段才被相加，它们的使用位置和生成位置相距甚远。为了解决这个问题，我们需要柯里化：函数不应该接受续体参数，而是返回一个「接受续体参数的函数」，也许我们可以叫它「续体对象」：

#lang racket
;;(+ (+ (* 2 3) 3) (- (/ 3 3) 1))
(define +**
  (λ (a) (λ (k0) (k0 (λ (b) (λ (k) (k (+ a b))))))))
(define -**
  (λ (a) (λ (k0) (k0 (λ (b) (λ (k) (k (- a b))))))))
(define ***
  (λ (a) (λ (k0) (k0 (λ (b) (λ (k) (k (* a b))))))))
(define /**
  (λ (a) (λ (k0) (k0 (λ (b) (λ (k) (k (/ a b))))))))

((((((((λ (k) (k 2)) ***) (λ (k) (k 3))) +**) (λ (k) (k 3))) +**)
  (((((λ (k) (k 3)) /**) (λ (k) (k 3))) -**) (λ (k) (k 1))))
 identity)
;;=> 9

尽管这段代码看起来更为繁琐，但我们不难发现它的组合性更好：

1. 首先计算 (+ (* 2 3) 3) ，即 (((((λ (k) (k 2)) ***) (λ (k) (k 3))) +**) (λ (k) (k 3))) ，记为 a1
2. 再计算 (- (/ 3 3) 1) ，即 (((((λ (k) (k 3)) /**) (λ (k) (k 3))) -**) (λ (k) (k 1))) ，记为 a2
3. 最后计算 (+ a1 a2) ，即 (((a1 +**) a2) identity)

现在，让我们来探讨单子与 CPS 之间的对应关系：

由此对应关系，我们可以实现 CPS 单子：

(define (Rc x) (λ (k) (k x))) ; unitM
(define (Cc m f) (m f))       ; bindM

是的，就是这么简单。

#lang racket

(define (Rc x) (λ (k) (k x))) ; unitM
(define (Cc m f) (m f))       ; bindM

;;(+ (+ (* 2 3) 3) (- (/ 3 3) 1))
(define +** (λ (a) (Rc (λ (b) (Rc (+ a b))))))
(define -** (λ (a) (Rc (λ (b) (Rc (- a b))))))
(define *** (λ (a) (Rc (λ (b) (Rc (* a b))))))
(define /** (λ (a) (Rc (λ (b) (Rc (/ a b))))))

((Cc
  (Cc (Cc (Cc (Cc (Cc (Rc 2) ***) (Rc 3)) +**) (Rc 3)) +**)
  (Cc (Cc (Cc (Cc (Rc 3) /**) (Rc 3)) -**) (Rc 1)))
 identity)

由此，我们便有了以 CPS 为基础的 CPS 单子 \(((λ(k)(k a)), Rc, Cc)\) ，我们会以它为基础编写一些代码。

;; -*- lexical-binding: t; -*-

(defalias 'λ 'lambda)
(defmacro Cc (m f)
  `(funcall ,m ,f))
(defmacro Rc (x)
  (let ((k* (gensym "$k")))
    `(λ (,k*) (funcall ,k* ,x))))
(defmacro Rc* (x) (if (atom x) (Rc x) x))
(defmacro +** () `(λ (a) (Rc (λ (b) (Rc (+ a b))))))
(defmacro -** () `(λ (a) (Rc (λ (b) (Rc (- a b))))))
(defmacro *** () `(λ (a) (Rc (λ (b) (Rc (* a b))))))
(defmacro /** () `(λ (a) (Rc (λ (b) (Rc (/ a b))))))
(defmacro my/+0 (a b)
  (let ((x (gensym "x"))
	(y (gensym "y")))
    `(Cc (Cc ,a (λ (,x) (Rc (λ (,y) (Rc (+ ,x ,y)))))) ,b)))
(defmacro my/+ (a b) `(Cc (Cc (Rc* ,a) (+**)) (Rc* ,b)))
(defmacro my/- (a b) `(Cc (Cc (Rc* ,a) (-**)) (Rc* ,b)))
(defmacro my/* (a b) `(Cc (Cc (Rc* ,a) (***)) (Rc* ,b)))
(defmacro my// (a b) `(Cc (Cc (Rc* ,a) (/**)) (Rc* ,b)))

;; test using
;; (macroexpand-all '(my/+ (my/+ (my/* 2 3) 3) (my/- (my// 3 3) 1)))

(my/+ (my/+ (my/* 2 3) 3) (my/- (my// 3 3) 1))
;;=> #[($k529) ((funcall $k529 (+ a b))) ((b . 0) (a . 9))]
(#[(k) ((funcall k (+ a b))) ((b . 0) (a . 9))] #'identity)
;;=> 9

#lang racket

(define-syntax-rule (Cc m f) (m f))
(define-syntax-rule (Rc x) (λ (k) (k x)))
(define-syntax (Rc* x)
  (syntax-case x ()
    [(k v) (if (list? (syntax-e #'v)) #'v #'(Rc v))]))
(define-syntax-rule (o** name op)
  (define-syntax-rule (name)
    (λ (a) (Rc (λ (b) (Rc (op a b)))))))
(define-syntax-rule (my/x name op)
  (define-syntax-rule (name a b)
    (Cc (Cc (Rc* a) (op)) (Rc* b))))

(begin
  (o** +** +) (my/x my/+ +**)
  (o** -** -) (my/x my/- -**)
  (o** *** *) (my/x my/* ***)
  (o** /** /) (my/x my// /**))

((my/+ (my/+ (my/* 2 3) 3) (my/- (my// 3 3) 1)) identity)
;;=> 9

就像我在上一小节结束时强调的，我们虽然实现了用于 CPS 代码的 unitM 和 bindM ，但并未对其类型做任何约束。练习 6 中的给出的四则运算函数的定义及其类型（这里的类型不怎么严谨）如下：

;; (-> number? (Cont (-> number? (Cont number?))))
(define +** (λ (a) (Rc (λ (b) (Rc (+ a b))))))
;; (-> (Cont any) (-> any (Cont any)) (Cont any))
Cc
;; (Cont (-> number? (Cont number?)))
(Cc (Rc 2) ***)
;; (Cont number?)
(Rc 3)
;; WTF?
(Cc (Cc (Rc 2) ***) (Rc 3))

在上面的最后一个表达式中，外层的 Cc 接受的第一个参数是续体对象，这没有问题。然而，它的第二个参数 应该 是一个续体函数，而不是续体对象。练习 6 中的代码之所以能够正常运行，是因为当时的续体对象和续体函数在代码层面没有实质区别。如果续体对象以其他形式实现，我们就必须加上使用续体对象调用对应续体函数的 runCont 函数：

(module Cont racket
  (define Cont%? (λ (x) (is-a? x Cont%)))
  (define Cont%
    (class object%
      (super-new)
      (init-field value)
      (define (call f) (value f))
      (define (call2 f) (value f))
      (public [call bindM] [call2 get])))
  (define (cont f) (instantiate Cont% [f]))
  (define (Gc m f) (send m get f))
  (define (Rc x) (cont (λ (k) (k x))))
  (define (Kc x) (λ (k) (k x)))
  (define (Cc m f) (send m bindM f))
  (define runCont Gc)
  (provide
   (contract-out
    [Cc (-> Cont%? (-> any/c Cont%?) Cont%?)]
    [Gc (-> Cont%? (-> any/c any/c) any/c)])
   Kc Rc runCont cont))

在上面的 Cont 模块中，我将续体对象实现为一个类 Cont% ，并使用 Racket 的 Contract 系统约束了 Cc 和 Gc (runCont) 接受的参数类型。如果我们尝试仅使用 Cc 或 Rc 构建代码，Contract 系统将会报告类型错误：

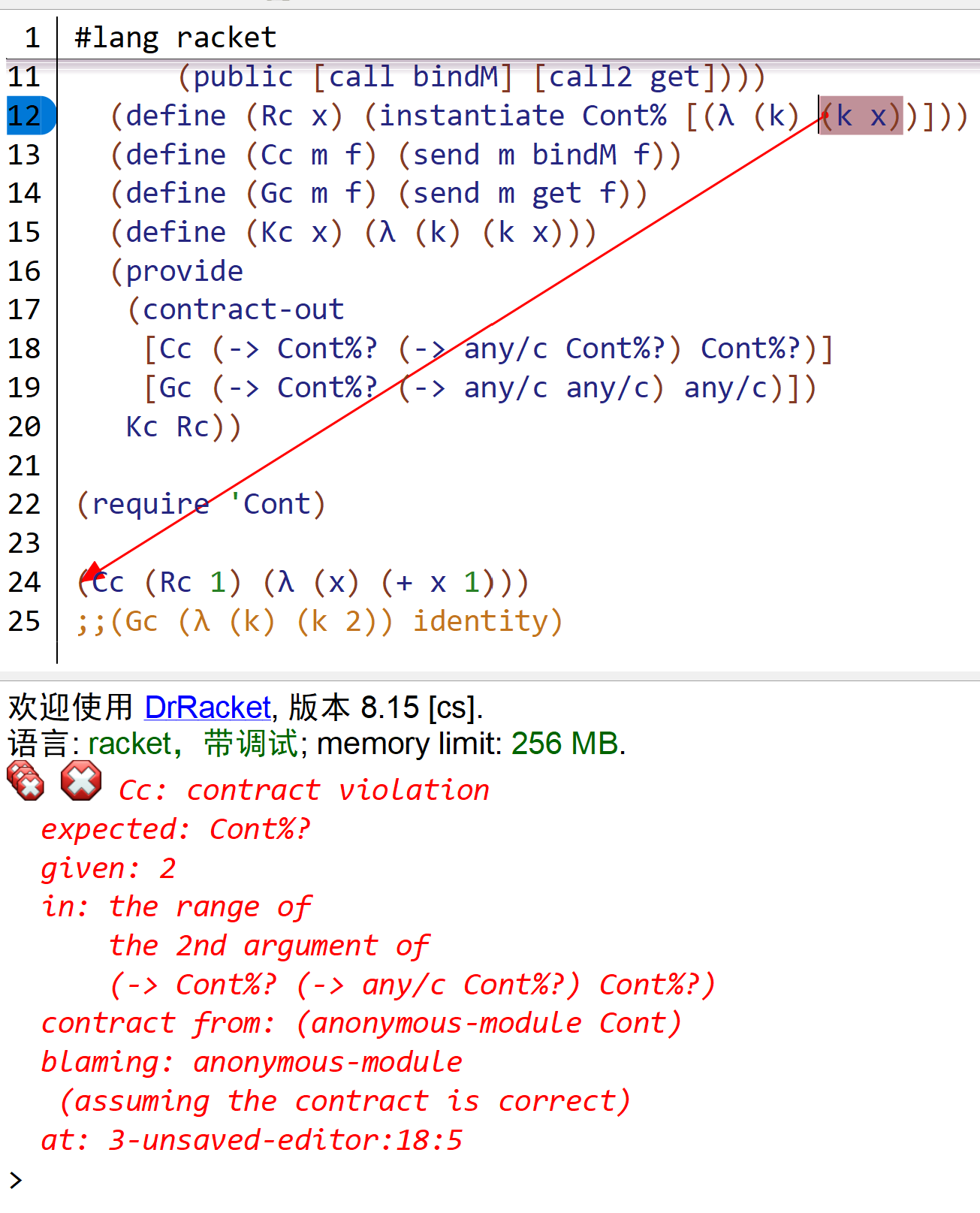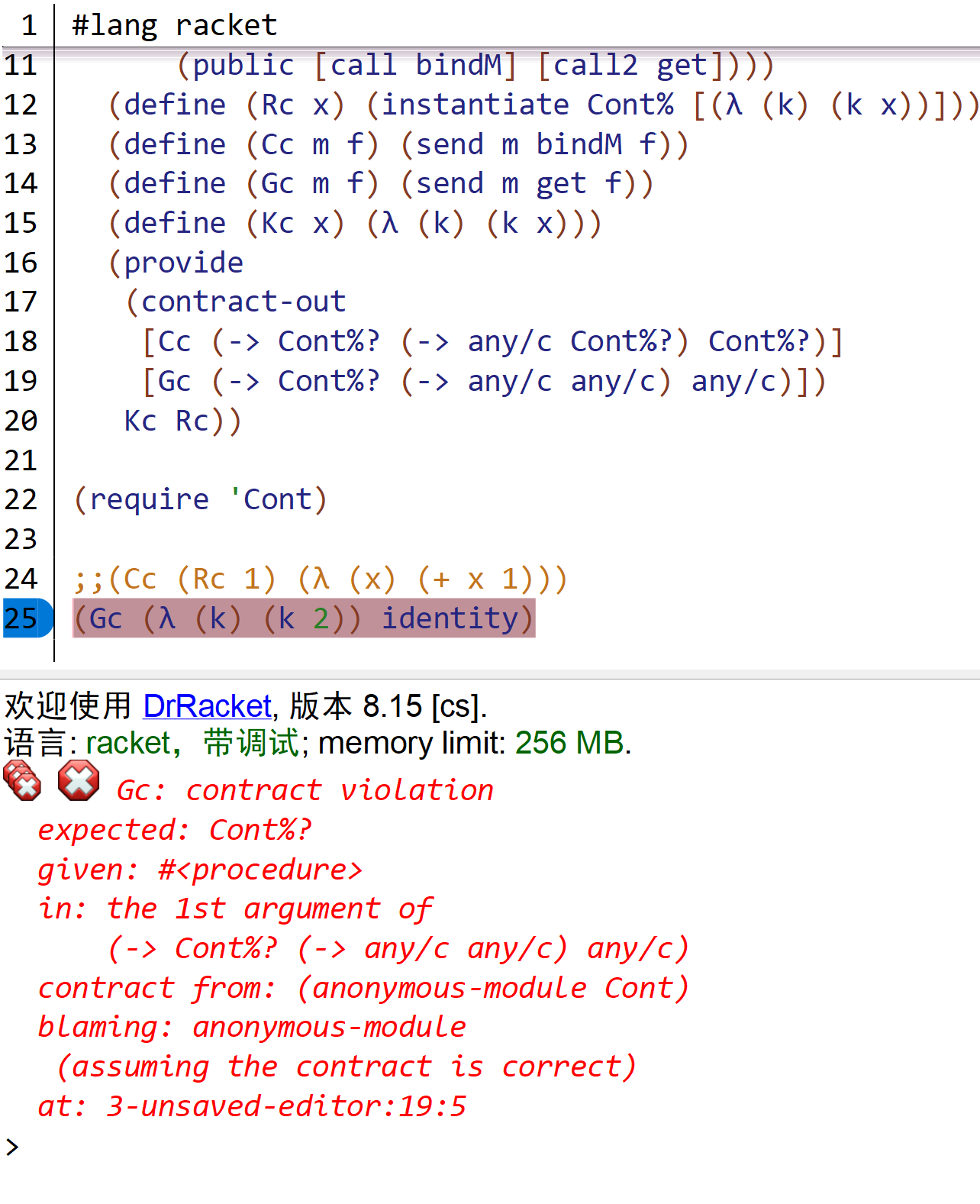现在，在类型正确的情况下，我们的代码将变为：

(require 'Cont)
(define-syntax-rule (gen/4 name op)
  (define name (λ (a) (Rc (λ (b) (Rc (op a b)))))))
(gen/4 +* +) (gen/4 -* -) (gen/4 ** *) (gen/4 /* /)

;;((Cc (Cc (Cc (Cc (Cc (Cc (Rc 2) ***) (Rc 3)) +**) (Rc 3)) +**)
;;     (Cc (Cc (Cc (Cc (Rc 3) /**) (Rc 3)) -**) (Rc 1)))
;; identity)
(Gc (Gc (Cc (Gc (Cc (Gc (Cc (Rc 2) **) (Kc 3)) +*) (Kc 3)) +*)
        (Gc (Gc (Cc (Gc (Cc (Rc 3) /*) (Kc 3)) -*) (Kc 1)) Kc))
    identity)

(require 'Cont)
(define-syntax-rule (gen/4 name op)
  (define name (λ (a b) (Rc (op a b)))))
(gen/4 +* +) (gen/4 -* -) (gen/4 ** *) (gen/4 /* /)

(require 'Cont)
(define-syntax-rule (gen/4 name op)
  (define name (λ (a b) (Rc (op a b)))))
(gen/4 +* +) (gen/4 -* -) (gen/4 ** *) (gen/4 /* /)

(Gc (Gc (Cc (** 2 3) (λ (x) (+* x 3)))
        (λ (x) (Gc (Cc (/* 3 3) (λ (x) (-* x 1)))
                   (λ (y) (+* x y)))))
    identity)

(Gc (Cc (Cc (** 2 3) (λ (x) (+* x 3)))
        (λ (x) (Cc (Cc (/* 3 3) (λ (x) (-* x 1)))
                   (λ (y) (+* x y)))))
    identity)

Wadler 在论文中给出的 Cont Monad 定义如下所示：

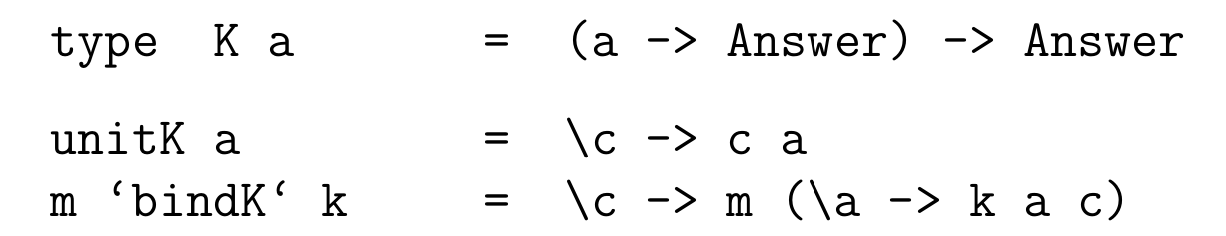
在上面的 Cond 模块中，我们将 bindM 实现为 (m f) 。Wadler 给出的定义实际上是显式化了整个调用过程，该定义只有在接收到续体后才会开始求值。相比之下，而我们实现的 (m f) 会立即进行部分求值，并返回一个等待接收续体参数的函数：

(define one (λ (k) (k 1)))
(define aone (λ (x) (λ (k) (k (+ x 1)))))

((one aone)
 identity) ;;=> 2
((λ (c) (one (λ (a) ((aone a) c))))
 identity) ;;=> 2

Wadler 的 bindK 定义更接近于 CPS 的本质，它将整个计算过程显式地通过续体传递来表达。这意味着 bindK 本身并不会立即执行任何计算，而是返回一个「等待接收续体的函数」。只有当续体被传递进来时，计算才会真正开始。这种方式更加符合 CPS 的思想，即所有的计算都由续体驱动。我们的方法虽然可以实现功能，但不是完全的 CPS 风格。我们可以如此改进 bindM 的实现：

(define (bindM f)
  (cont (λ (c) (Gc this (λ (a) (Gc (f a) c))))))

(module Cont racket
  (define Cont%? (λ (x) (is-a? x Cont%)))
  (define Cont%
    (class object%
      (super-new)
      (init-field value)
      (define (call f) (value f))
      (define (bindM f)
        (cont (λ (c) (Gc this (λ (a) (Gc (f a) c))))))
      (public bindM [call get])))
  (define (cont f) (instantiate Cont% [f]))
  (define (Gc m f) (send m get f))
  (define (Rc x) (cont (λ (k) (k x))))
  (define (Kc x) (λ (k) (k x)))
  (define (Cc m f) (send m bindM f))
  (define runCont Gc)
  (provide
   (contract-out
    [Cc (-> Cont%? (-> any/c Cont%?) Cont%?)]
    [Gc (-> Cont%? (-> any/c any/c) any/c)])
   Kc Rc runCont cont))

在 3.2 节，Wadler 给出了捕获当前续体的 callCC 的定义：

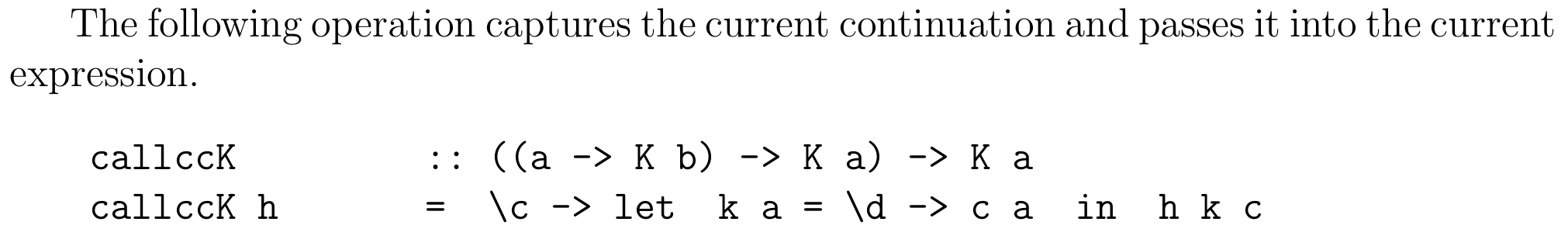
如果 Haskell 的匿名函数记号看不习惯我这里还有经典 lambda 演算版的：

\[[[call/cc]] = λf.λk.f(λv.λk_0.kv)k\]

请注意 Haskell 定义中的 (let k a = \d -> c a) 和 lambda 演算定义中的 (λv.λk0.kv) ，它们与单位续体 (λ (x) (λ (k) (k x))) 非常相似。然而，在 call/cc 中，单位续体的 k0 被省略了，仅使用来自 call/cc 调用处的 k ，这导致函数 f 在使用自身的续体参数时，会将控制流返回到 call/cc 的调用位置。我们可以在 Cont 模块中按如下方式实现 callCC ：

(define (callCC f)
  (cont (λ (k) (Gc (f (λ (v) (cont (λ (_k) (k v))))) k))))

#lang racket

(module Cont racket
  (define Cont%? (λ (x) (is-a? x Cont%)))
  (define Cont%
    (class object%
      (super-new)
      (init-field value)
      (define (call f) (value f))
      (define (bindM f)
        (cont (λ (c) (Gc this (λ (a) (Gc (f a) c))))))
      (public bindM [call get])))
  (define (cont f) (instantiate Cont% [f]))
  (define (Gc m f) (send m get f))
  (define (Rc x) (cont (λ (k) (k x))))
  (define (Kc x) (λ (k) (k x)))
  (define (Cc m f) (send m bindM f))
  (define runCont Gc)
  (define (callCC f)
    (cont (λ (k) (Gc (f (λ (v) (cont (λ (_k) (k v))))) k))))
  (provide
   (contract-out
    [Cc (-> Cont%? (-> any/c Cont%?) Cont%?)]
    [Gc (-> Cont%? (-> any/c any/c) any/c)]
    [callCC (((any/c . -> . Cont%?) . -> . Cont%?) . -> . Cont%?)])
   Kc Rc runCont cont))

(require 'Cont)

;; ((λ (k) (k 1)) (λ (x) (λ (k) (k (+ x 1)))))
(Gc (Cc (Rc 1) (λ (x) (Rc (+ x 1)))) identity) ;;=> 2
;; (call/cc (λ (k) (k (+ 2 3))))
(Gc (callCC (λ (k) (k (+ 2 3)))) identity) ;;=> 5
(Gc (callCC (λ (k) (Cc (Rc 2) (λ (x) (k (* x 3)))))) identity) ;;=> 6
(Gc (callCC (λ (k) (Rc (* 1 2)))) identity) ;;=> 2

(require 'Cont)

(define (product ls k)
  (Gc (callCC
       (λ (k0)
         (let f ([ls ls] [k k0])
           (cond
             ((null? ls) (k 1))
             ((zero? (car ls)) (k0 0))
             (else
              (display (car ls))
              (f (cdr ls) (λ (v) (k (* v (car ls))))))))))
      k))
(product '(1 2 3) list)
;;=> 123'(6)
(product '(1 2 0 3) list)
;;=> 12'(0)

(define (product* ls k)
  (Gc (let f ([ls ls] [m (Rc 1)])
        (cond
          ((null? ls) m)
          ((zero? (car ls)) (Rc 0))
          (else
           (display (car ls))
           (f (cdr ls) (Cc m (λ (v) (Rc (* v (car ls)))))))))
      k))
(product* '(1 2 3) list)
;;=> 123'(6)
(product* '(1 2 0 3) list)
;;=> 12'(0)

-- written by GPT4

import Control.Monad.Trans.Cont
import Control.Monad

productCont :: [Int] -> Int
productCont xs = runCont (callCC $ \exit -> foldM (step exit) 1 xs) id
  where
    step :: (Int -> Cont r Int) -> Int -> Int -> Cont r Int
    step exit acc x
      | x == 0    = exit 0
      | otherwise = return (acc * x)

test1 :: IO ()
test1 = do
  print "test1"
  print $ productCont []                -- 1
  print $ productCont [1, 2, 3, 4]      -- 24
  print $ productCont [1, 2, 0, 4]      -- 0
  print $ productCont [0, 1, 2, 3, 4]   -- 0

-- CPS written by GPT4
productCont2 :: [Int] -> Int
productCont2 xs = runCont (cpsProduct xs) id

cpsProduct :: [Int] -> Cont r Int
cpsProduct []     = return 1
cpsProduct (x:xs) =
  if x == 0
  then return 0
  else do
    rest <- cpsProduct xs
    return (x * rest)
test2 :: IO ()
test2 = do
  print "test 2"
  print $ productCont2 []                -- 1
  print $ productCont2 [1, 2, 3, 4]      -- 24
  print $ productCont2 [1, 2, 0, 4]      -- 0
  print $ productCont2 [0, 1, 2, 3, 4]   -- 0

Programming with monads strongly reminiscent of continuation-passing style (CPS), and this paper explores the relationship between the two. In a sense they are equivalent: CPS arises as a special case of a monad, and any monad may be embedded in CPS by changing the answer type. But the monadic approach provides additional insight and allows a finer degree of control.

在续体单子中， bindM (Cc) 操作的作用是将计算结果传递给一个新的函数，这个函数表示后续的计算。具体来说， bindM 操作将一个续体对象 m 和一个续体函数 c 结合，得到一个新的续体对象。它在形式上可以表示为 (Cc m c) 。如果我们对 Cc 进行柯里化， (Cc m) 得到的是一个接受续体函数并返回新的续体对象的函数，即 (λ (c) (Cc m c)) 。根据下面的定义你会发现这个形式已经是一个续体对象了。我们可以定义一个根据普通单子得到续体对象的函数 promote ，它将普通单子转换为续体单子：

对于任何普通的单子，我们都有一种将它“嵌入”到续体单子中的方法，即 (cont (λ (c) (m . bindM . c))) 。需要注意的是，在续体单子中，续体函数本身就代表了 整个 单子后续的计算，这个特点在其他单子中不一定成立。因为除将计算结果传递给后续的计算函数 c ，其他单子的 bindM 操作可能涉及一些额外的操作（例如状态修改、错误处理、异步操作等）。由于额外操作的存在，通过 bindM 操作符绑定到某个单子的函数 c 实际上只构成了该单子计算的「续体的一部分」。

考虑到除续体单子外，所有单子的 bindM 都会执行一些额外的操作，仅仅调用续体函数的续体单子应该是 最基础的单子类型 。通过将普通单子转换为续体单子，我们让普通单子与续体单子的区别变得 更加明显 。这一过程就像是浅层的 CPS 转换，因为我们只是将普通单子的计算结果包装成一个接受并调用续体函数的形式，而没有深入到整个计算的控制流。正如浅层的 CPS 转换只是通过引入一个额外的函数来控制计算流，而不改变计算的核心结构一样，普通单子被转换为续体单子后，仍然保持了它原有的计算逻辑，只是通过续体的方式来组织和处理结果。

在这一节中，我们首先介绍了单子的定义和实现方式，并以单位单子和列表单子作为例子进行说明。接着，我们将 CPS 代码柯里化并封装为续体单子，在此过程中考虑了类型问题和惰性求值，并不断对实现进行改进。最后，我们讨论了续体单子的特殊性： 所有的单子都能转换为续体单子 ，这背后的语言续体机制是所有组合性的基础。

由于在单子的 bind 操作中，并不是将单子的所有计算过程暴露给续体函数，而是仅暴露当前计算的部分结果，因此我们可以利用单子自然地实现处理逻辑与计算逻辑的分离，避免将两者耦合在一起。

Given the results of the previous section, one may wonder whether there is any real difference between monads and CPS. … There is a difference. Each of the monad types we have described may be turned into an abstract data type, and that provides somewhat finer control than CPS.

在论文的 3.4 节，Wadler 讨论了 CPS 和 Monad 的区别，它认为 Monad 能做到更好的模块化，如果全用 CPS 可能会滥用续体的逃逸能力，但我们可以选择是否为某种 Monad 提供这种能力。

Perhaps a more significant difference between monads and CPS is the change of view point. Monads focus attention on the question of exactly what abstract operations are required, what laws they satisfy, and how one can combine the features represented by different monads.

下面是一些介绍 Haskell 中 Cont Monad 用法的文章，感兴趣同学可以看看：

• Haskell/Continuation passing style, Continuation与Call/CC by 苟富
• Continuation 与 monad by lsdsjy
• 聊一聊Haskell中的MonadCont by Kell

老实说，写到这里我们已经完全明白什么是单子了，但为了让读者和我熟悉它的简单用法，在本文的下一节跟着 Wadler 论文的第二章学习一些常见的单子吧。

在前文的 Cont 单子中我们使用 Rc 和 Cc 来表示单子的 unitM 和 bindM 操作，如果我们为所有的类都实现了 bindM 和 unitM ，我们就可以使用如下函数来实现通用的 return 和 >>= ：

(define (return m a) (send m return a))
(define (>>= m fun) (send m bind fun))

为了确保实现的类带有这两个方法，我们可以使用接口进行约束：

(define Monad0<%> (interface ()))
(define Monad/c (is-a?/c Monad0<%>))
(define Monad<%>
  (interface (Monad0<%>)
    [return (->m any/c Monad/c)]
    [bind (->m (-> any/c Monad/c) Monad/c)]))

但是，那些可以被当作单子的基础类型呢？我们只能对对象调用 send ，但是从头实现或者包装一遍基础函数又有点太蠢了。一种方法是在 >>= 中判断参数类型调用对应基础类型的 bind 实现，Monads in Dynamically-Typed Languages 似乎给出了更好的方法：tonyg/monad.rkt。

参考 tonyg (Tony Garnock-Jones) 给出一个合理的 Racket Monad 实现似乎可以单独作为一篇博客。

在得到一个好用的 Monad 接口后，我们可以在 Racket 中尝试实现各种简单的单子。但光是实现一遍没什么用，重要的是与其他语言中的相似特性，或者是一些编程中的最佳实践（比如 Maybe 单子与尽早返回 (early return)）进行关联来帮助理解。我计划就以下单子写一篇或多篇博客：

实现一个正确的 Monad 当然重要，但是更重要的可能是理解单子后面的抽象，我们在编写代码时很可能已经用上了这些抽象但没意识到。通过单子来显式化这些东西是应该是能够让我们明白怎么写更好的代码的。目前我能想到的可能只有 C++ 的 std::optional 和 std::expected ，Rust 的 Option 和 Result 和 JavaScript 的 ? 系列语法。在写这些单子博客的过程中应该能发现更多。

你好奇单子之间怎么组合吗？我反正挺好奇的。

在本文开头提到的论文 Introduction to Programming with Shift and Reset 中，作者使用 shift/reset 这一种有界续体操作符实现了状态单子：

#lang racket
(require racket/control)

(define my-car (λ (x) (car x)))
(define (call-counter f)
  (λ args
    (shift k (λ (ini-state)
               ((k (apply f args)) (+ 1 ini-state))))))

(define (getter)
  (shift k (λ (state) ((k state) state))))

(define b (call-counter my-car))
((reset (let ((res (list (cons (b '(1 2)) (b '(2 3))) (getter))))
          (λ (v) res)))
 0)
;;=> '((1 . 2) 2)

上面的代码在没有引入副作用的情况下实现了统计 my-car 调用次数的装饰器 call-counter 。也许所有的单子都能用有界续体来表示或者实现？Capturing the Future by Replaying the Past。

Delimited continuations are the mother of all monads!

So, what is actually an "Effect" in Haskell? Essentially, that is what most of the programmers used to call "Aspect" — any property additional to a primary concept. Yes, that is very abstract.

— What Is An Effect In Functional Programming by 7mind

在很多教程中你可以看到这样的对单子的描述：单子就是用来实现副作用的/单子被用来隔离副作用/单子被用来包装副作用。首先，在一门纯函数式语言中我们不可能实现副作用，所以第一种观点是显然错误的；后两种观点不能说错误，但是太过片面了，因为副作用只是「作用」的一种，而且单子并不是仅仅用来处理副作用。

为了了解什么是「作用」，也许我们需要学一门支持 algebraic effect 的语言，比如 Koka（こうか、効果）。